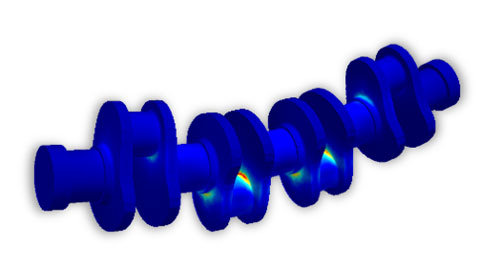
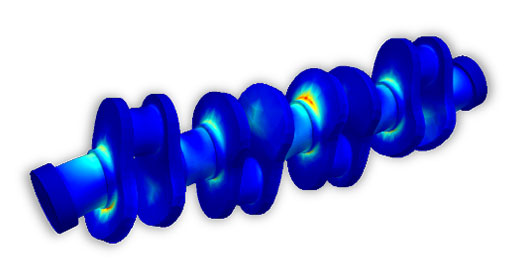
Hochlaufsimulation eines 4-Zylinder Triebwerks
Einleitung
Im Hinblick auf die moderne Produktentwicklung stellt die Simulation ein unverzichtbares Werkzeug dar. Sie ermöglicht eine effiziente Vorauslegung einzelner Bauteile bis hin zur Analyse von komplexen Baugruppen. Auch in der Triebwerksdynamik finden sich zahlreiche Einsatzmöglichkeiten für Simulationsaufgaben. Eine zentrale Anwendung ist zum Beispiel die Betriebsfestigkeit der Bauteile. Die rechnerische Lebensdauerabschätzung hilft der sicheren und wirtschaftlichen Auslegung von Komponenten. NVH und Akustik sind weitere Anwendungsgebiete, in denen die Simulation zum Verständnis der Systemdynamik dient.
Die in der Simulation ermittelten Lagerkräfte können z.B. für akustische Analysen einen entscheidenden Beitrag leisten, wo sich die Anregung des Motorblocks in der Schallabstrahlung widerspiegelt. Auch die Schwingungsanregung bzw. Resonanzeffekte unterschiedlicher Anbauteile des Motors können mit Hilfe der Simulation geklärt werden und ersetzen somit kostspielige Dauerlaufversuche.
Flexible Körper
Der erste Schritt in Richtung einer MKS-Simulation besteht in der Vernetzung und der modalen Reduktion der flexiblen Körper. Dabei werden die Verschiebungen und Spannungen als Linearkombination von modalen Koordinaten dargestellt. Während die modale Basis der Verschiebung für die Modellierung des flexiblen Körpers zwingend notwendig ist, werden die modalen Spannungen nur für eine nachgelagerte Betriebsfestigkeitsanalyse benötigt.
Das vorliegende Beispiel beschränkt sich auf die flexible Modellierung der Kurbelwelle. Die Mindestanzahl der erforderlichen Moden richtet sich grob nach der Zielrichtung der Analyse. Werden die Modelle beispielsweise vorwiegend für Torsionsschwingungsanalysen oder für akustische Fragestellungen verwendet, können die höheren Moden der modalen Reduktion vernachlässigt werden. Steht hingegen die Ermittlung der Spannungen im Fokus, sind die hochfrequenten Moden zu berücksichtigen, da sie die lokalen Deformationen beschreiben und damit den Spannungsverlauf an den kritischen Stellen wesentlich beeinflussen.
Modale Reduktion der Kurbelwelle
Für Detailuntersuchungen an Pleuel, Kolben, Dämpfer oder Schwungrad können diese Bauteile in gleicher Weise als flexible Körper behandelt werden. Für alle anderen Fragestellungen, in denen die Gesamtdynamik des Systems im Vordergrund steht, ist die Modellierung im Sinne eines Starrkörpers ausreichend.
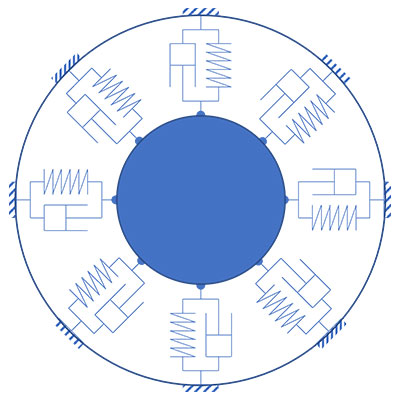
Lagerstellen
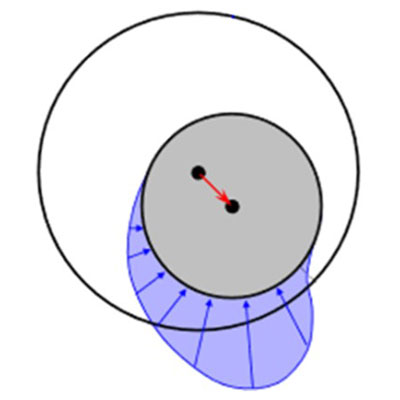
Ein besonderes Augenmerk richtet sich auf die Modellierung der Lagerstellen. Zum breiten Spektrum der Möglichkeiten die Kraftelemente zu beschreiben, gehören z.B. ideale kinematische Bindungen, lineare oder nichtlineare Feder-Dämpfer, Kennfeldlösungen für die Ersatzsteifigkeiten und zwei- oder dreidimensionale hydrodynamischen Gleitlagermodelle.
3D & 2D EHD oder Feder-Dämpfer-Lagermodelle
Die Auswahl richtet sich dabei nicht nur nach der angrenzende Modellierungstiefe der verbindenden Bauteile, sondern auch nach der Zielrichtung der Simulationsaufgabe. Im Falle einer flexiblen Kurbelwelle sind beispielsweise zur Lagerung elastische Kraftelemente notwendig. Ideale Bindungsgleichungen an den Lagerstellen zum Kurbelgehäuse würden in diesem Fall das System deutlich versteifen. Die rein kinematische Ankopplung eines starren Pleuels ist hingegen zulässig und im Sinne einer effizienten Simulation auch sinnvoll.
Im Hinblick auf die Ankopplung von Kraftelementen an elastische Strukturen sei noch eine weitere Problematik zu erwähnen. Während sich die Modellierung von Kraftangriffsstellen im Sinne der Starrkörpermechanik als trivial erweist, sind die Schnittstellen für Kräfte und Momente an flexible FE-Körper mathematisch sehr komplex und vielfältig. Je nach Anforderung unterscheidet man zwischen flexiblen Modellierungselementen oder kinematischen Bindungen. Zu beachten ist jedoch, dass der lineare Charakter einer modalen Reduktion die Modellierung der Schnittstellen ebenfalls nur auf lineare Elemente beschränkt.
Gasdrücke
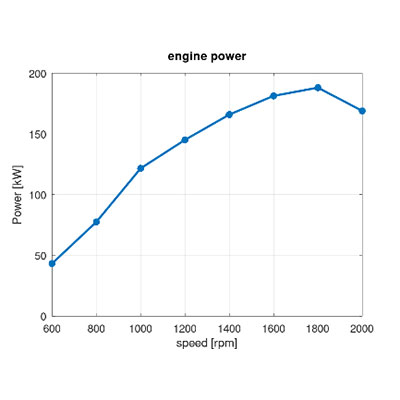
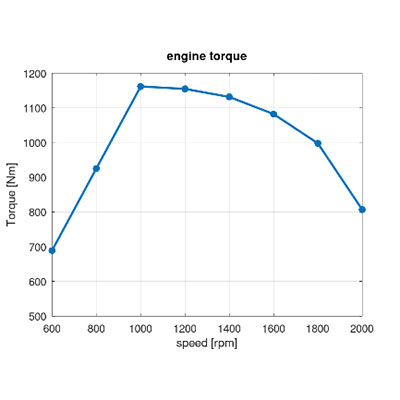
Als Anregung des Systems dienen gemessene oder synthetische Gasdruckverläufe, die in der Regel als Funktion des Kurbelwinkels dargestellt werden. Gerade bei messtechnisch erfassten Gasdrücken führen Messfehler oft zu unterschiedlichen Verläufen zwischen den einzelnen Zylindern, Abweichungen vom Spitzendruck oder zu einer leichten Phasenverschiebung. Bei der Aufprägung der Belastung in Abhängigkeit vom Kurbelwinkel ist weiterhin zu beachten, dass die torsionale Verformung der Kurbelwelle oft eine nicht zu unterschätzende Phasenverschiebung zwischen den einzelnen Zylindern bewirkt. Auch die Umrechnung der Gasdrücke mit Hilfe der Kurbelkinematik in Moment und Leistung ist zur Überprüfung der Motordaten sinnvoll.
Gasdrücke, stationäres Motormoment und Leistung
Schwingungsdämpfer
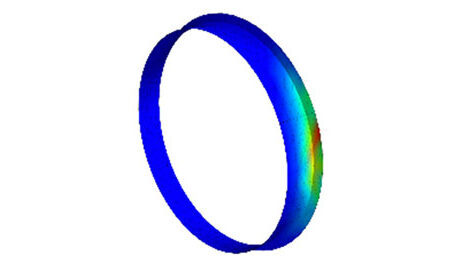
Torsionsschwingungsdämpfer haben die Aufgabe, die im Betrieb unvermeidbaren Drehschwingungen einer Kurbelwelle zu bedämpfen. Ein Viskodämpfer besteht aus einem mit der Kurbelwelle verbundenem Primärteil und einer sekundärseitigen Schwungmasse in Form eines Ringes, der im Gehäuse drehbar gelagert ist. Zwischen dem Gehäuse und dem Dämfperring befindet sich eine viskose Dämpferflüssigkeit, die bei einer Relativbewegung die Flüssigkeit auf Scherung beansprucht, was gleichzeitig einen Dämpfungseffekt bedeutet.
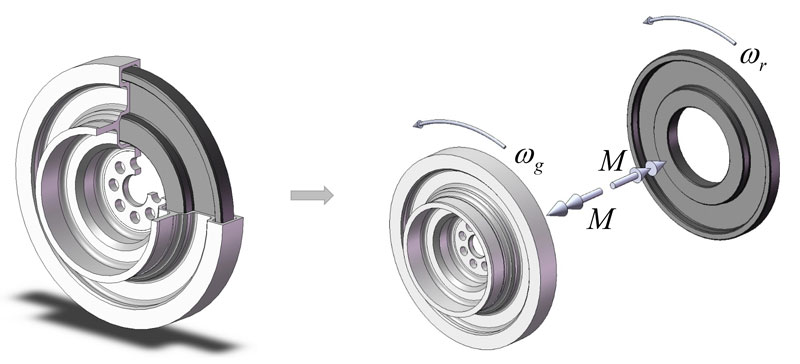
Aufbau eines Schwingungsdämpfers
Aus mechanischer Sicht, wirkt ein Viskodämpfer bei konstanten Betriebsbedingungen mathematisch wie ein paralleles Feder-Dämpfer-Element (Voigt-Kelvin-Element). Die wesentliche Eigenschaft eines Viskodämpfers ist jedoch eine von der Frequenz und Temperatur abhängige Steifigkeit und Dämpfung. Die klassische Auslegung von Torsionsschwingungssystemen erfolgt in der Regel über lineare Modelle im Frequenzbereich. Hier bereiten Modelle eines Viskodämpfers rechnerisch keine Schwierigkeiten. Führt man beispielsweise eine Frequenzgangrechnung durch, so ist lediglich die frequenzabhängige Steifigkeit und Dämpfung des Feder-Dämpfer-Elements zu berücksichtigen.
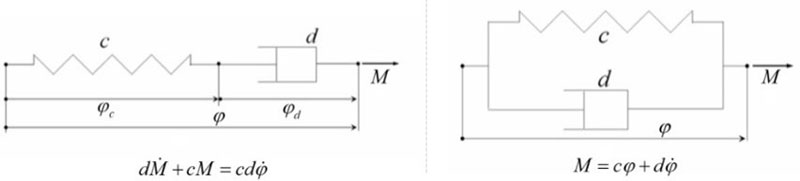
Maxwell- (links) und Voigt-Kelvin-Element (rechts)
Das viskoelastische Materialverhalten des Dämpfers wird im Zeitbereich über rheologische Ansätze in Form von Maxwell-Elemente realisiert. Während ein paralleles Feder-Dämpfer-Element aus Sicht der Mehrkörperdynamik ein typisches Kraftelement in Form einer algebraischen Gleichung darstellt, handelt es sich bei einem Maxwell-Element um eine Differentialgleichung erster Ordnung. Somit führt jedes Maxwell-Element einen eigenen Zustand ein und erst die Lösung der DGL liefert das Moment in Abhängigkeit von der relativen Bewegung. In der Praxis unterzieht man i.R. die Elemente ebenfalls einer numerischen Integration.
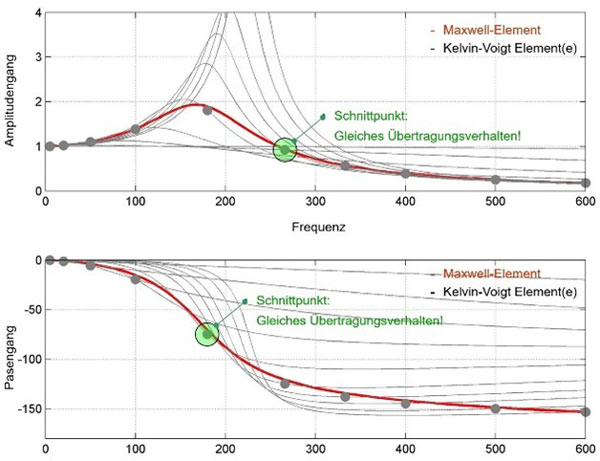
Ansatz für Parameterbestimmung
Während das mechanische Modell eines Viskodämpfers recht einfach aufgebaut ist, ist die Parameterbestimmung der generalisierten Maxwell-Elemente nicht trivial. Zu einer Lösung führt der Ansatz, dass für jede Frequenz und Temperatur im Betriebsbereich das generalisierte Maxwell-Element ein identisches Übertragungsverhalten wie ein Voigt-Kelvin-Element zeigen soll. Über den gesamten Betriebsbereich gelingt das natürlich nur näherungsweise. Diese Überlegung führt dabei zu einem nichtlinearen Optimierungsproblem im Sinne eines least-squares-Ansatzes. Dabei steigt der numerische Aufwand mit der Anzahl der Maxwell-Stränge und Betriebspunkte.
Torsionsschwingungsanalysen
Der Kurbeltrieb zusammen mit den Anbauten am vorderen und hinteren Ende eines Verbrennungsmotors stellt ein schwingungsfähiges System dar. Bei der Grundauslegung eines Triebwerks sind vor allem die Torsionsschwingungen der Kurbelwelle zu beachten, die bei Resonanzdurchgängen bzw. längerem Betreiben des Motors in den Resonanzdrehzahlen zu Torsionsbrüchen führen können.
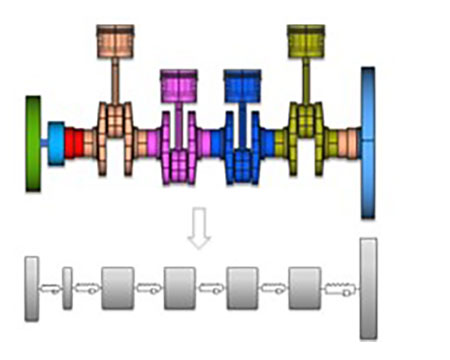
Torsionsschwinger als Ersatzmodell
Die klassische Auslegung eines Triebwerks erfolgt über lineare Torsionsschwingungsmodelle im Frequenzbereich. Dazu wird zunächst ein Ersatzsystem im Sinne eines linearen Mehrmassenschwingers abgeleitet und mit Hilfe einer Modalanalyse bzw. Frequenzgangrechnung untersucht. Als Anregung des linearen Systems dienen die Fouriertransformationen der gemessenen oder synthetisch erzeugten Gasdrücken. Betrachtet man das reduzierte System als linearen Torsionsschwinger, so können damit die auftretenden Torsionsmomente an den kritischen Punkten ermittelt werden. Dazu zählen z.B. Kupplung, Schwungrad- oder Dämpferverschraubung.
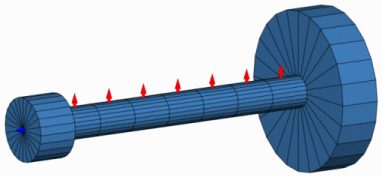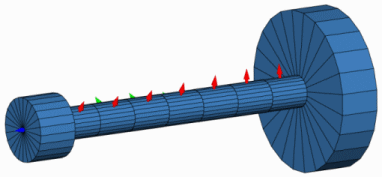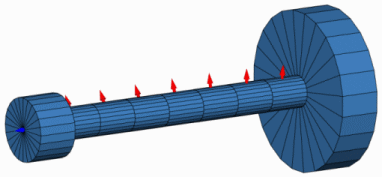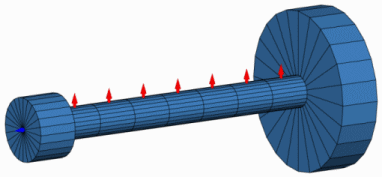
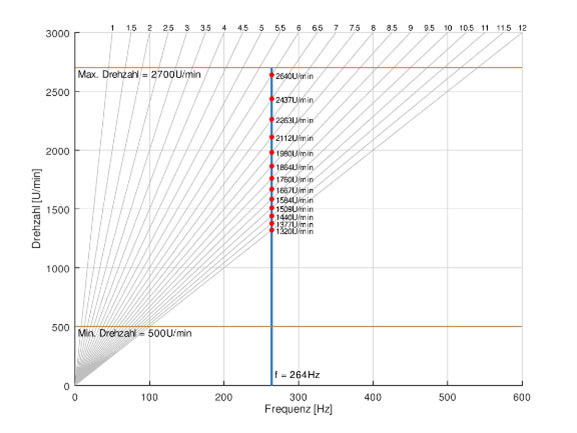
Schwingform der 3ten Torsionseigenfrequenz
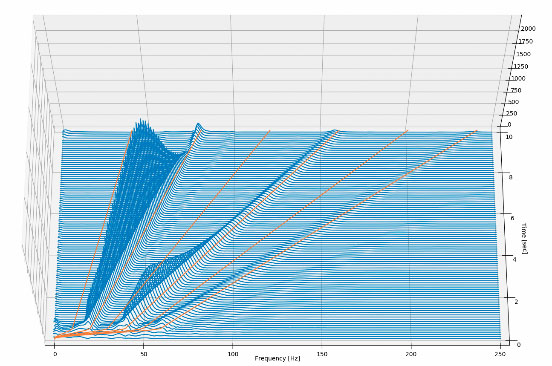
Beispielhaft dargestellt ist die erste relevante Schwingform der 3. Torsionseigenfrequenz bei ungefähr 264 Hz. Zeichnet man diese als senkrechte Gerade in das Campbell-Diagramm ein, so erkennt man an den Schnittpunkten mit den Ordnungsstrahlen, dass eine Resonanzanregung in diesem Beispiel im Drehzahlbereich von 500-2700 U/min erst ab der 6. Ordnung möglich ist.
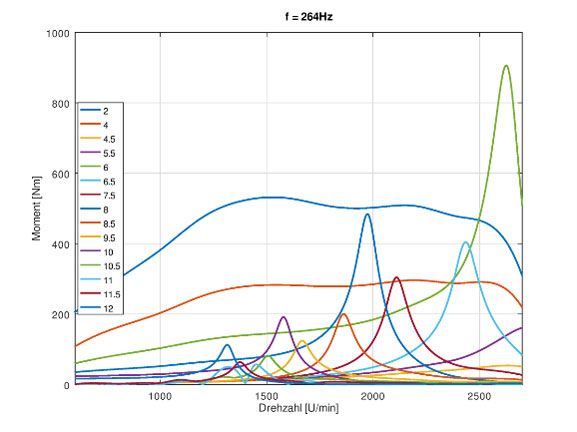
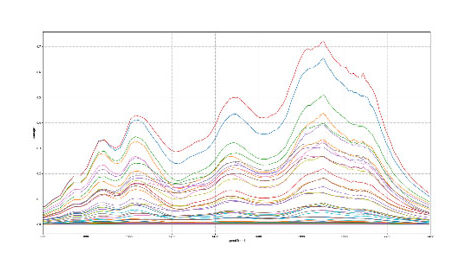
Die Ordnungsanalyse dient vorwiegend zur Ermittlung von Resonanzdrehzahlen und deren Auswirkung auf die Amplituden sämtlicher Schnittgrößen. Hier dargestellt ist die Ordnungsanalyse des Torsionsmomentes an der Schwungradverschraubung. Betrachtet man die einzelnen Ordnungen, so sind die Resonanzlagen zu erkennen, die hier hauptsächlich durch die 6te, 6,5te, 7,5te und 8te Ordnung hervorgerufen werden. Dabei wird jeweils die in der Animation gezeigte 3te Eigenfrequenz bei 264 Hz angeregt.
Die lineare Frequenzganganalyse richtet den Fokus ausschließlich auf die unvermeidbaren Torsionsschwingungen des Antriebstranges. Sind tiefere Einblicke in die Systemdynamik des Triebwerks von Interesse, sind die Methoden der Mehrkörperdynamik die geeigneten Werkzeuge.
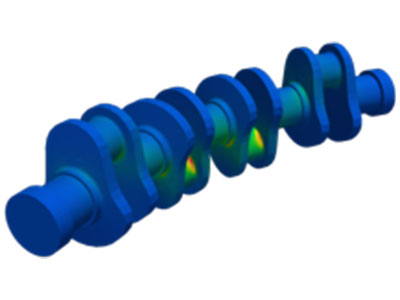
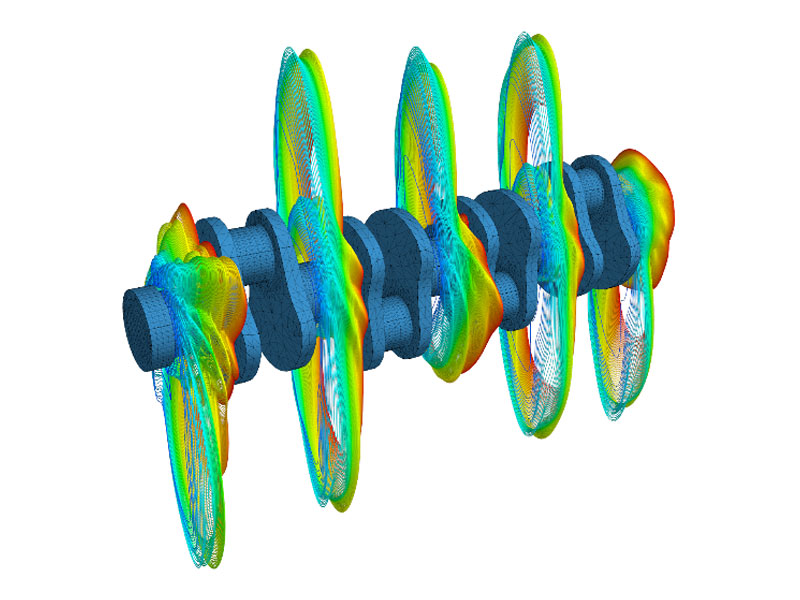
MKS-Hochlaufsimulation

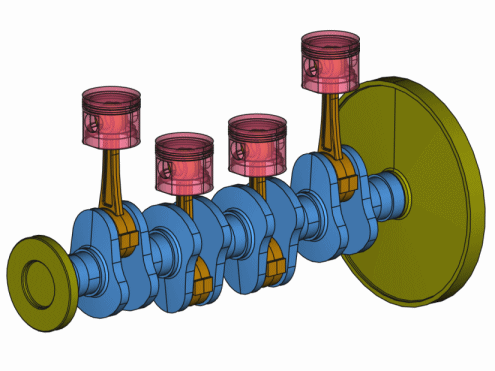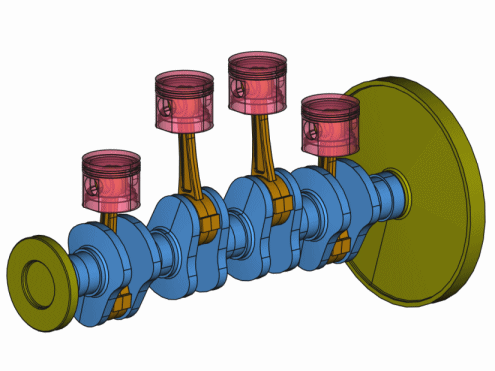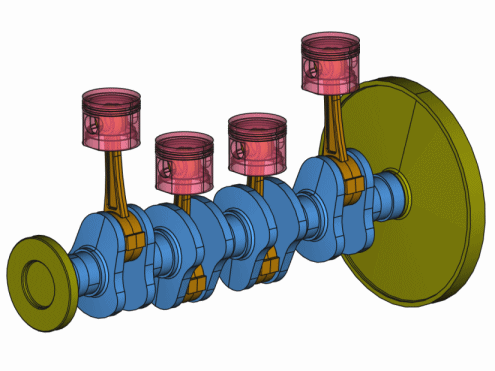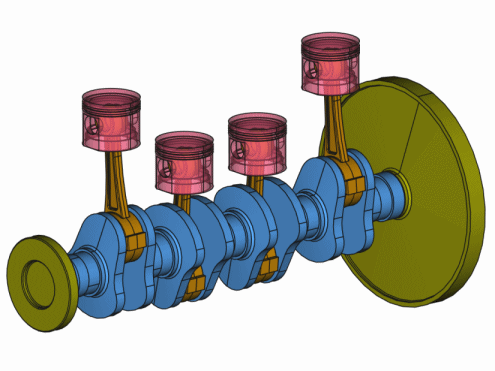
Animation eines 4-Zylindertriebwerks mit flexibler Kurbelwelle
Eine typische Anwendung der MKS-Simulation ist die Ermittlung von Bauteilbelastungen und in Zusammenspiel mit der FEM ein unverzichtbares Werkzeug zur Auslegung beliebiger Bauteile hinsichtlich Betriebsfestigkeit, Lebensdauer oder Akustik.
Komplexe Systeme wie das vorliegende Triebwerk zeigen bei verschiedenen Drehzahlen, Betriebsbedingungen und -zuständen auch deutlich unterschiedliche Belastungen der Komponenten. Um diese kritischen Betriebspunkte zu ermitteln, bedient man sich einer sog. Hochlaufsimulation. Diese erlaubt die Ermittlung sämtlicher Schnittgrößen über den gesamten Drehzahlbereich hinweg.
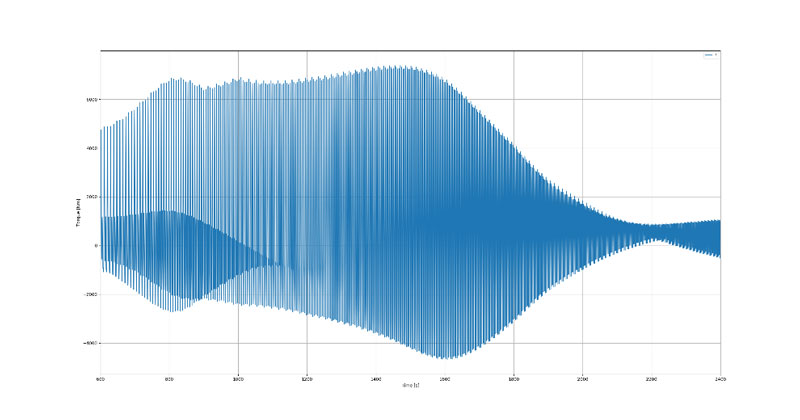
Während die messtechnische Erfassung bestimmter Größen in der Praxis sehr eingeschränkt ist, ermöglicht die Simulation tiefe Einblicke in die Systemdynamik. Betrachtet man beispielsweise die Hauptlagerkräfte des vorliegenden Triebwerks, so ist deren Ermittlung messtechnisch kaum zu realisieren. Im Gegensatz dazu, ermöglichen Simulationsmodelle die problemlose Berechnung sämtlicher Schnittgrößen an beliebigen Stellen und Betriebspunkten.
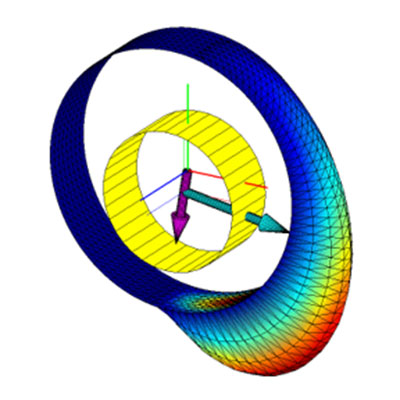
Das folgende Beispiel zeigt die Amplituden der Hauptlagerkräfte in polarer Darstellung abgewickelt über die Lagerbreite. Dabei wird deutlich, dass sich wegen der Flexibilität der Kurbelwelle die Kraftverläufe in Ihrer Amplitude und Phase deutlich unterscheiden.

Amplituden der Hauptlagerkräfte in polarer Darstellung
Für Detailuntersuchungen an diversen Komponenten sind oft nur einzelne Betriebspunkte relevant. Eine intuitive Festlegung dieser kritischen Zustände führt in der Praxis oft zu falschen Annahmen und damit zu großen Unsicherheiten im Hinblick auf die Auslegung der Komponenten.
Folgendes Beispiel macht diesen Sachverhalt deutlich. Aus den Kennfelder des Motors erkennt man am Verlauf des mittleren Momentes und der mittleren Leistung zwei Betriebspunkte, in denen Moment bzw. Leistung ein Maximum bei einer Drehzahl von etwa 1000 bzw. 1800 U/min aufweisen. Die intuitive Wahl dieser beiden Betriebspunkte (maximales Moment und maximale Leistung) als Auslegungskriterium erweist sich bei näherer Betrachtung als fehlerhaft.
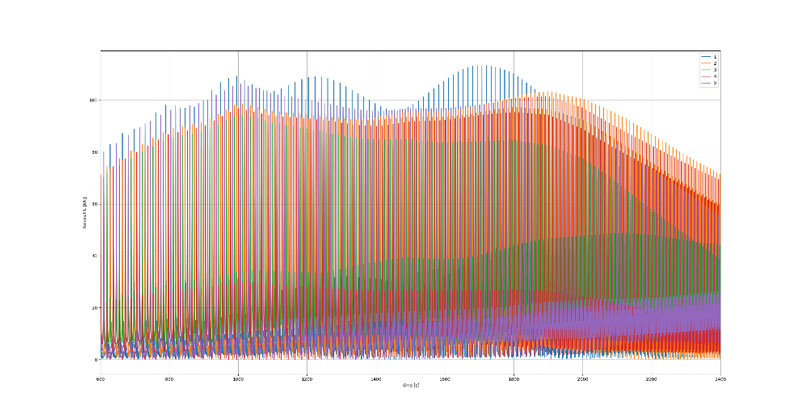
Torsionsmoment und Hauptlagerkräfte
Wirft man einen tieferen Blick in die Systemdynamik des Triebwerks, so lässt sich beobachten, dass im Falle des transienten Torsionsmomentes eine maximale Amplitude bei einer Drehzahl von etwa 1500 U/min zu erwarten ist. Auch die Hauptlagerkräfte zeigen je nach Lagerstelle bei unterschiedlichen Drehzahlen maximale Amplituden. Für Hauptlager 1 liegt das Maximum z.B. bei etwa 1700 U/min und bei Hauptlager 2 ist es eine Drehzahl von etwa 1900 U/min. Somit wird deutlich, dass für die Auslegung unterschiedlicher Komponenten auch unterschiedliche Betriebspunkte relevant sind, die nur durch einen tieferen Einblick in die Systemdynamik mit Hilfe der MKS-Simulation zu erkennen sind.
Auch im Hinblick auf akustische Analysen und Untersuchungen zur Schwingungsanregung von Anbauteilen leisten Simulationsmodelle einen wesentlichen Beitrag.
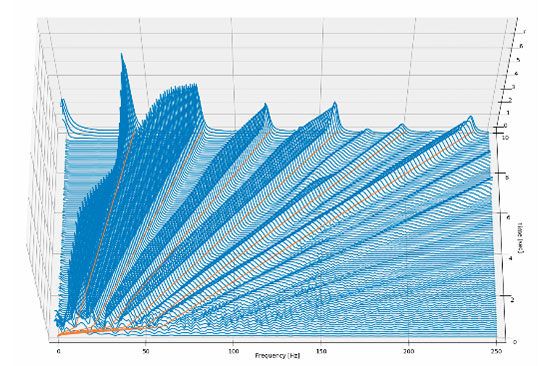
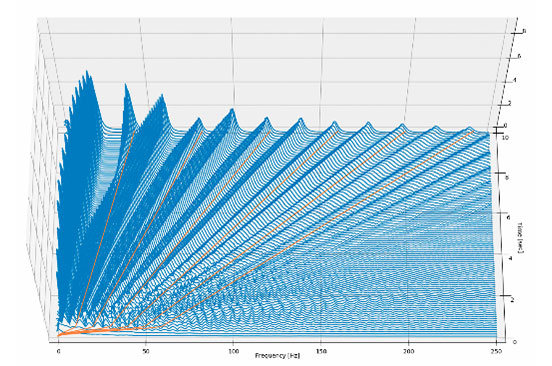
FFT-Analyse des Torsionsmomentes und der Hauptlagerkräfte 3 bzw. 5
In den FFT-Analysen des Torsionsmomentes und der Hauptlagerkräfte 3 bzw. 5 erkennt man z.B. den unterschiedlichen Frequenzinhalt der Schnittgrößen, die als Anregung der flexiblen Struktur des Kurbelgehäuses zu sehen sind. Während das Torsionsmoment hauptsächlich die Hauptordnungen des Triebwerks aufweist, treten bei den Lagerkräften auch signifikante Nebenordnungen auf. Dies macht deutlich, dass erst mit der Kenntnis des gesamten Anregungsspektrums verlässliche Aussagen hinsichtlich Akustik oder Schwingungsanregung möglich sind.
Betriebsfestigkeit
Allein die Kenntnis des Spannungszustandes an den kritischen Stellen ist nicht ausreichend für eine sichere Aussage im Hinblick auf die Betriebsfestigkeit der Bauteile. Stützwirkung, Oberflächenbehandlung, Materialeigenschaften, usw. haben einen signifikanten Einfluss auf die Lebensdauer der Komponenten. Eine Analyse im Sinne einer Betriebsfestigkeit ist somit für die endgültige Komponentenabsicherung eine zwingende Voraussetzung.
Vergleicht man z.B. den Spannungsverlauf an den gefährdeten Stellen des Hauptlagers 5 mit dessen Schädigung über den gesamten Drehzahlbereich, so wird deutlich, dass erst die vollständige Untersuchung im Sinne einer Lebensdaueranalyse die wahre Belastung und die kritische Stelle und Betriebspunkt zum Vorschein bringt.
Spannungen, Schädigungen und kritische Stelle
Die Betriebsfestigkeit ist aus Sicht der Simulation als ein reiner Post-Processing-Schritt zu sehen. Dabei werden die Spannungen aus der Linearkombination der modalen Basis mit den modalen Koordinaten berechnet und anschließend mit klassischen Methoden der Lebensdaueranalyse behandelt. Die wesentliche Problematik bei der modalen Reduktion ist dabei die exakte Abbildung der lokalen Verformung und damit des Spannungszustandes an kritischen Stellen. Während modale Eigenformen mit niedriger Frequenz eher globale Verformungen darstellen, beschreiben Moden mit hoher Frequenz eher lokale Verformungen und Spannung. Während für die grobe Beurteilung der Systemdynamik höhere Moden vernachlässigbar sind, muss im Hinblick auf die Spannungen die modale Basis ausreichend erweitert werden.
Erste und eine höhere Eigenform der modalen Basis und die entsprechenden Spannungen
Eine nachgelagerte Detailanalyse an einem Teilmodell mittels FEM schafft in diesem Zusammenhang oft eine zuverlässige Abhilfe. Ein Vergleich des modalen Spannungszustandes mit dem der linearen FE-Teilrechnung liefert einen Hinweis über die Güte der modalen Approximation.
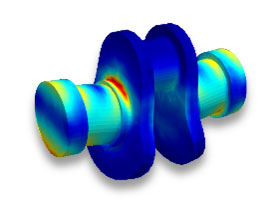
FE-Teilrechnung
Zusammenfassung
Das vorliegende Beispiel beabsichtigt die vielfältigen Einsatzmöglichkeiten der Simulation im Hinblick auf die Entwicklung und Optimierung komplexer Systeme zu skizzieren. Obwohl die messtechnische Untersuchung technischer Systeme in der Erprobung unverzichtbar ist, stößt sie jedoch an praktische Grenzen. Gewisse Größen, die für die optimale Auslegung relevant sind, sind messtechnisch oft nicht zugänglich. Aufwändige Dauerlaufversuche sind nicht nur sehr kostspielig, sie widerspiegeln oft nur eingeschränkt die im Betrieb auftretenden Betriebszustände.
Viele Fragestellungen können mit Hilfe der Simulation geklärt werden. Sie erlaubt einen tiefen Einblick in die Systemdynamik und dient damit nicht nur der optimalen Auslegungen von Bauteilen, sondern ist auch für das Systemverständnis ein unverzichtbares Werkzeug.
Dieses Beispiel deutet ebenfalls an, dass in der Praxis eine problemangepasste Modellierungstiefe sinnvoll ist. Auch die ausgewählten Methoden und Modellierungselemente richten sich in der Regel nach der vorliegenden Simulationsaufgabe. Diese Vorgehensweise ist nicht nur aus Gründen der numerischen Effizienz notwendig, sondern richtet auch den Fokus der Untersuchung gezielt auf die wesentlichen Effekte und leistet damit einen entscheidenden Beitrag zum Systemverständnis.