Rotordynamik von Turbolader mit Schwimmbuchsenlagerung
Abgasturbolader werden vorwiegend in modernen Verbrennungsmotoren zur Steigerung des thermodynamischen Wirkungsgrades eingesetzt. Um optimale Betriebsbedingungen zu erreichen, sind aufgrund der geringen Baugröße hohe Drehzahlen erforderlich. In diesem Zusammenhang spielt die Lagerung eine besondere Rolle. Bei diesen hochtourigen Rotoren werden oft hydrodynamische Lager eingesetzt, die gegenüber anderen Lagerungsarten wie Wälz- bzw. Magnetlager gewisse Vorteile aufweisen. Neben einer langen Lebensdauer und geringen Kosten, sind vor allem die besseren Dämpfungseigenschaften zu nennen.
Gleitlager
Die wesentliche Problematik im Hinblick auf die rotordynamischen Eigenschaften von gleitgelagerten Läufern, sind die unvermeidbaren Instabilitätserscheinungen der Gleitlager durch ölfilminduzierte selbsterregte Schwingungen. Die wesentliche Ursache dafür ist die Tatsache, dass die Lagerkraft W und die Zapfenverschiebung u aufgrund des asymmetrischen Druckverlaufs nicht parallel verlaufen.
Eine vertikale Belastung der rotierenden Welle führt zu einer horizontalen Komponente der Auslenkung. Man spricht in diesem Zusammenhang von schiefsymmetrischen Eigenschaften der Steifigkeitsmatrix als Ursache für instabiles Verhalten.
Instabilitäten sind somit bei einer Gleitlagerung ab einer gewissen Grenzdrehzahl grundsätzlich vorhanden. Folgendes Simulationsbeispiel soll diesen Sachverhalt verdeutlichen.
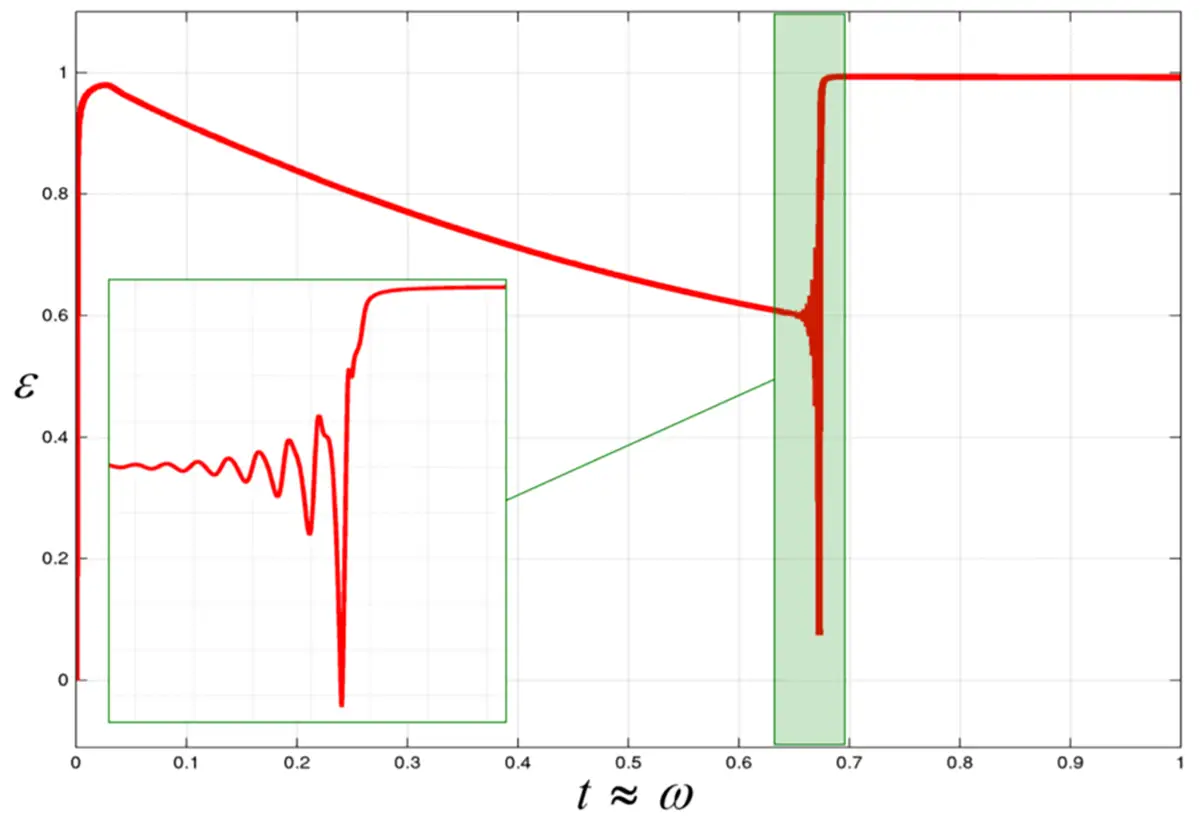
Eine gleitgelagerte Welle wird unter Gewichtskrafteinfluss rotatorisch beschleunigt. Mit steigender Drehzahl steigt auch die Tragfähigkeit des Lagers, womit die Exzentrizität bis zu einem gewissen Wert fällt. Überschreitet die Welle die kritische Drehzahl, so führen kleine Störungen zur Instabilität des Systems. Das Lager verliert sprunghaft seine Tragfähigkeit und nimmt einen sog. Grenzzyklus ein, in dem die Welle mit hoher Exzentrizität umläuft. Dabei ist die Umlauffrequenz niedriger als die Drehzahl der Welle. Man spricht in diesem Zusammenhang von subsynchronen Schwingungen.
Zapfenverschiebung und Druckverlauf eines Gleitlagers
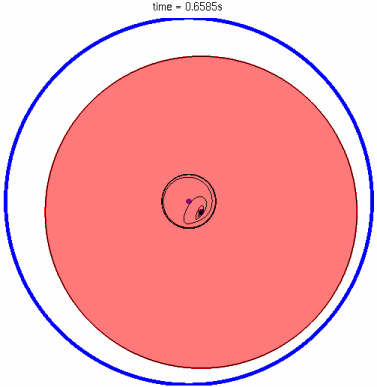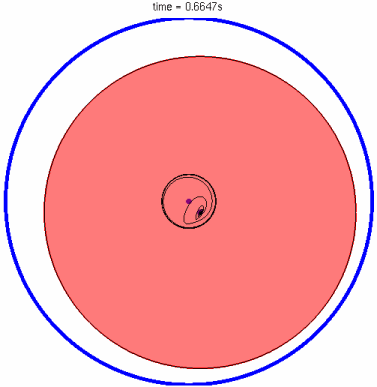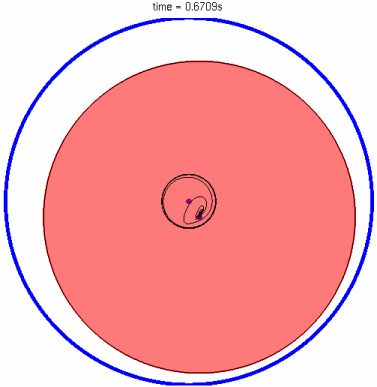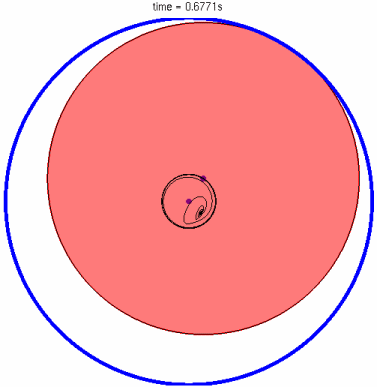
Animation des Hochlaufs (links) und Exzentrizität des Gleitlagers (rechts)
Schwimmbuchsenlager
Ein Schwimmbuchsenlager ist eine spezielle Bauform eines Gleitlagers. Zwischen Wellenzapfen und Lagergehäuse befindet sich eine frei drehbare Buchse, so dass sich ein innerer und ein äußerer Schmierfilm ergibt. Durch diese Aufteilung der Schmierfilme erreicht man eine Reduzierung der effektiven Drehzahl und verschiebt damit die kritischen Betriebspunkte hin zu höheren Drehzahlen.
Wie in der Animation dargestellt, ist das wesentliches Merkmal dieser Lagerung jedoch die gegenseitige Beeinflussung der beiden Schmierfilme.
Ein optimales Auslegungsziel ist dann erreicht, wenn die unvermeidbaren Instabilitätserscheinungen des inneren bzw. äußeren Ölfilms durch den jeweils anderen ausreichend gedämpft werden. Bleiben die zugehörigen Amplituden innerhalb gewisser Grenzen, so ist weiterhin ein sicherer Betrieb des Rotors gewährleistet. Jedoch können Betriebszustände erreicht werden, in denen die Amplituden der selbsterregten Schwingungen unzulässig hohe Werte annehmen und damit zu einem Schaden führen.
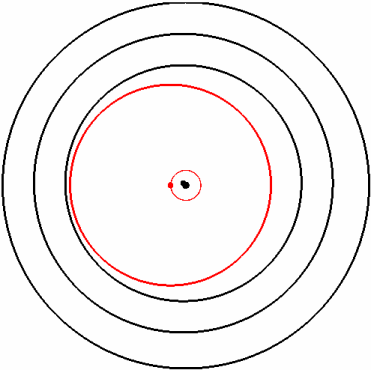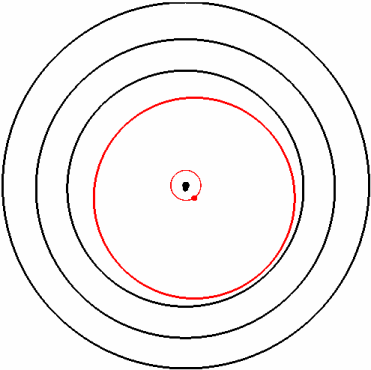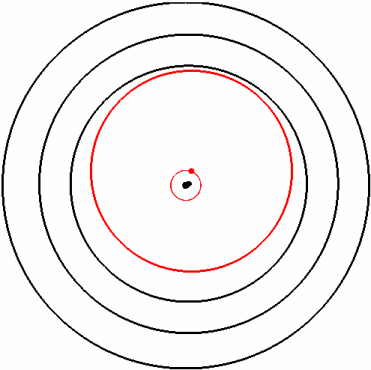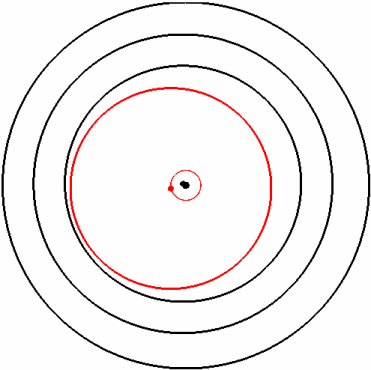
Animation des Hochlaufs (links) und Aufbau des Schwimmbuchsenlagers (rechts)
Simulationsmethoden
Solche Effekte können vorab in der Simulation untersucht und Gegenmaßnahmen abgeleitet werden. Eine detaillierte Stabilitätsuntersuchung mit den Methoden der numerischen Bifurkationsanalyse, die zur Bestimmung der stabilen bzw. instabilen Lösungen und die Detektierung der Bifurkationspunkte eingesetzt werden kann, ist sehr komplex, aufwendig und oft nur für akademische Beispiele anwendbar.
In der Praxis haben sich im Hinblick auf die Auslegung rotordynamischer Systeme zwei unterschiedliche Methoden etabliert: die lineare Frequenzganganalyse und die transiente Hochlaufsimulation. Es sei jedoch anzumerken, dass zuverlässige Absolutaussagen in der Praxis oft nicht möglich sind. Im Hinblick auf die geometrische Auslegung solcher Systeme ist es sinnvoller und zielführender, ausgehend von einem an Messungen abgestimmtes Modell, Relativaussagen durch Variation einzelner Parameter zu verfolgen.
Modellbildung
Die verwendeten MKS-Modelle bestehen in der Regel aus einer modal reduzierten Welle und starren Turbinenräder. Die Schwimmbuchsen sind im Idealfall als Starrkörper modelliert, die über hydrodynamische Gleitlagerroutinen an das Gehäuse bzw. Welle angebunden sind. Um die im Betrieb auftretenden Instabilitäten numerisch zuverlässig zu erfassen, sind analytische Berechnungsroutinen sinnvoll, die frei von einer numerischer Diskretisierung sind und damit weniger anfällig für numerische Artefakte bzw. Rundungsfehler.

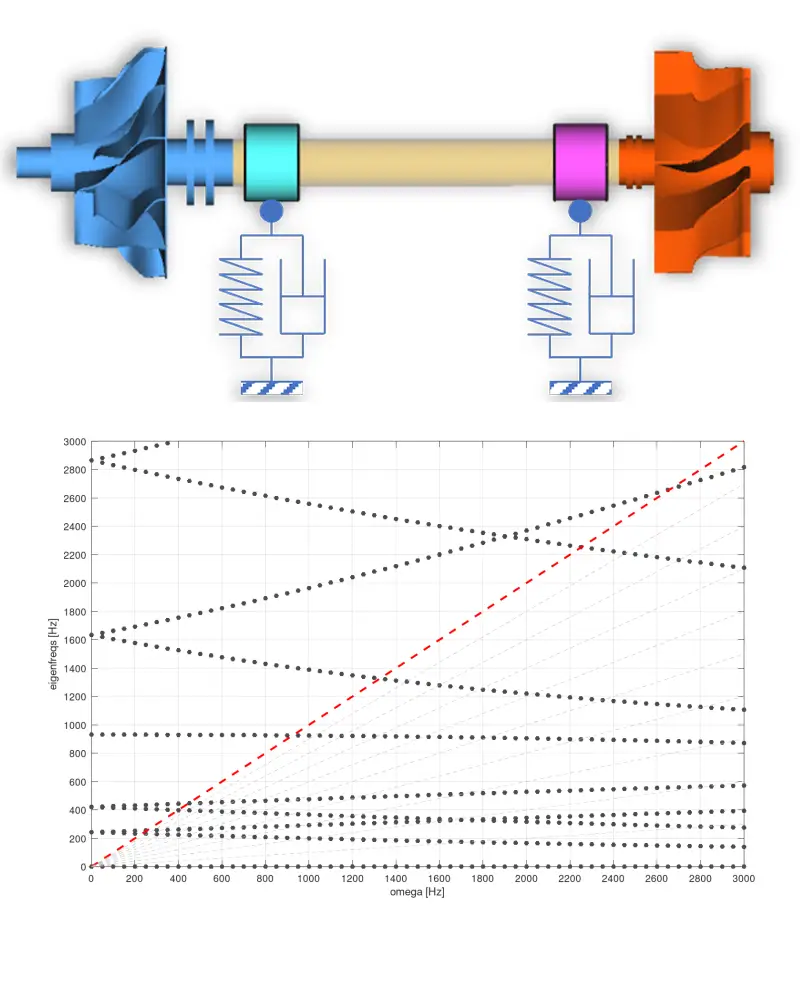
Modellskizze eines Turboladers
Während das mechanische System in seiner Komplexität überschaubar bleibt und sich mit Standardmethoden der Mehrkörperdynamik modellieren lässt, ist die geeignete Abbildung der Hydrodynamik hier als die wesentliche Problematik zu sehen.
Die Impedanz-Methoden, die mit vorberechneten Steifigkeits- und Dämpfungskennfelder arbeiten, erweisen sich in diesem Zusammenhang als ungeeignet. Für mechanische Systeme die nur kleine Bewegungen um eine quasi-statische Ruhelage zeigen, dürfen linearisierte Gleitlagerkräfte angewendet werden. Dies ist z.B. bei schweren Turbinen der Fall, bei denen die Welle durch ihr hohes Eigengewicht in die quasi-statische Ruhelage gedrückt wird. Die Linearisierung um diesen Betriebspunkt ist in diesem Fall zulässig und die lineare Theorie anwendbar.
Bei allen Systemen, bei denen die nichtlinearen Ölfilmkräfte eine entscheidende Rolle spielen, versagt die lineare Theorie und es müssen die exakten Kraft-Bewegungs-Beziehungen berechnet werden. Diskretisiert man die zugrundeliegende hydrodynamische Grundgleichung mit Finite-Element- oder Finite Differenz-Methoden, lässt sich über die anschließende numerische Integration das Kraft-Bewegungsgesetz zuverlässig ermitteln. Diese Vorgehensweise ist aber im Hinblick auf die Hochlaufsimulation sehr aufwendig und nicht frei von numerischen Störungen.
Die sog. analytischen Gleitlagermethoden schaffen in diesem im Zusammenhang Abhilfe. Durch die Annahme von gewissen Vereinfachungen lässt sich eine rein analytische Lösung für die nichtlinearen Gleitlagerkräfte finden. Diese entscheidende Tatsache erlaubt effiziente Simulationen bei geringem Verlust an Genauigkeit.
Unwucht
Neben den ölfilminduzierten selbsterregten Schwingungen, stellt die Unwucht eine entscheidende Anregung des Systems dar. Es ist praktisch möglich, die Turbinen- und Verdichterräder im Sinne eines Starrkörpers auszuwuchten, der gesamte Rotor wegen seiner Flexibilität jedoch nicht. Hinzu kommt, dass jede De- bzw. Montage des Rotors seinen Unwuchtszustand ändert. Weiterhin spielen auch thermoelastische Effekte während des Betriebs eine zentrale Rolle. Die exakte Unwucht in einem Simulationsmodell abzubilden ist aus den o.g. Gründen nicht möglich.
Folgendes Beispiel soll verdeutlichen, wie die angenommene Unwucht die Lagerkräfte und somit die Systemdynamik entscheidend prägt.
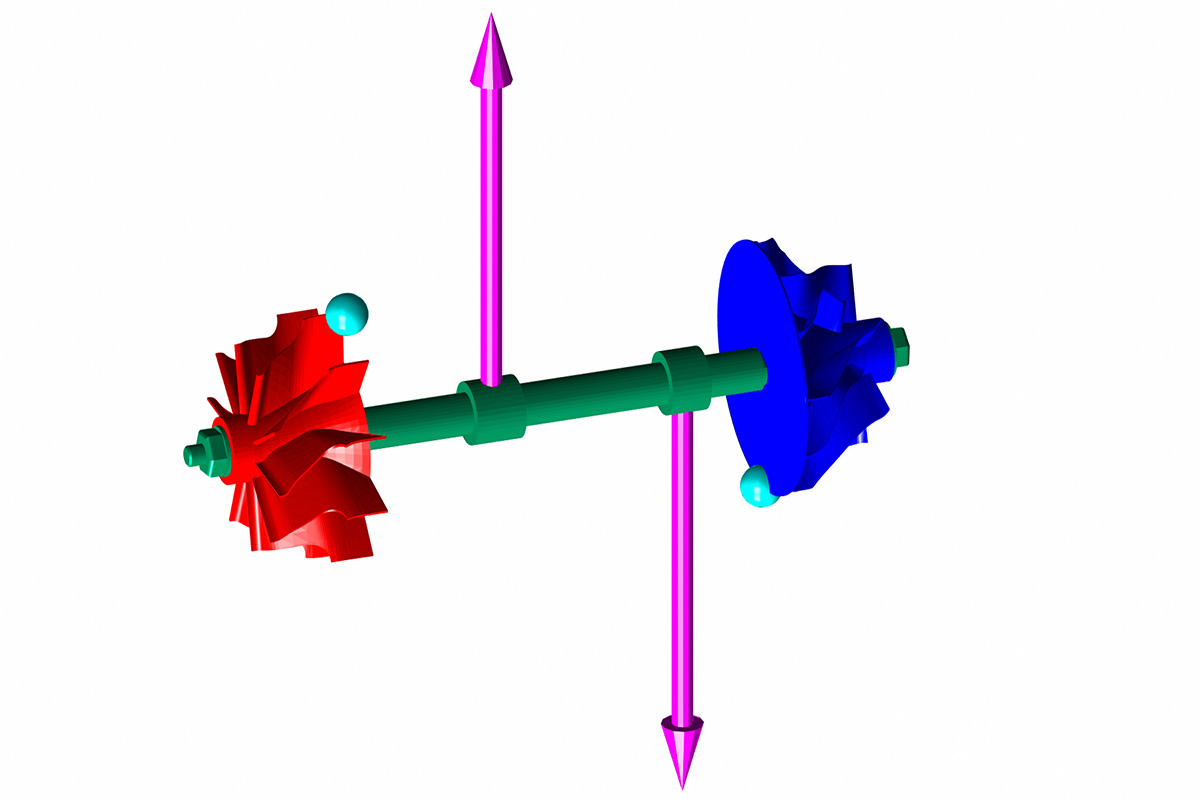
Dargestellt sind maßstäblich die Lagerkräfte bei unterschiedlicher Unwucht: statische Unwucht, dynamische Unwucht und eine beliebige Mischform. Deutlich zu erkennen ist die unterschiedliche Richtung und Amplitude der Lagerkräfte für einen stationären Betriebspunkt.
Lineare Frequenzganganalyse
In rotordynamischen Systemen hängen die Eigenfrequenzen aufgrund von Kreiseleffekten oder variablen hydrodynamischen Bedingungen in Gleitlagern von der Drehzahl ab. Diese rotordynamischen Systeme zeigen somit ein stark nichtlineares Verhalten und lassen sich somit nicht zuverlässig mit der linearen Theorie behandeln. In der Praxis ist es trotzdem oft sinnvoll, diese Systeme zu linearisieren und im Sinne einer Eigenwertanalyse mit gyroskopischem Einfluss zu untersuchen. Damit lässt sich gezielt der Einfluss unterschiedlicher Parameter im Hinblick auf kritische Drehzahlen prüfen.
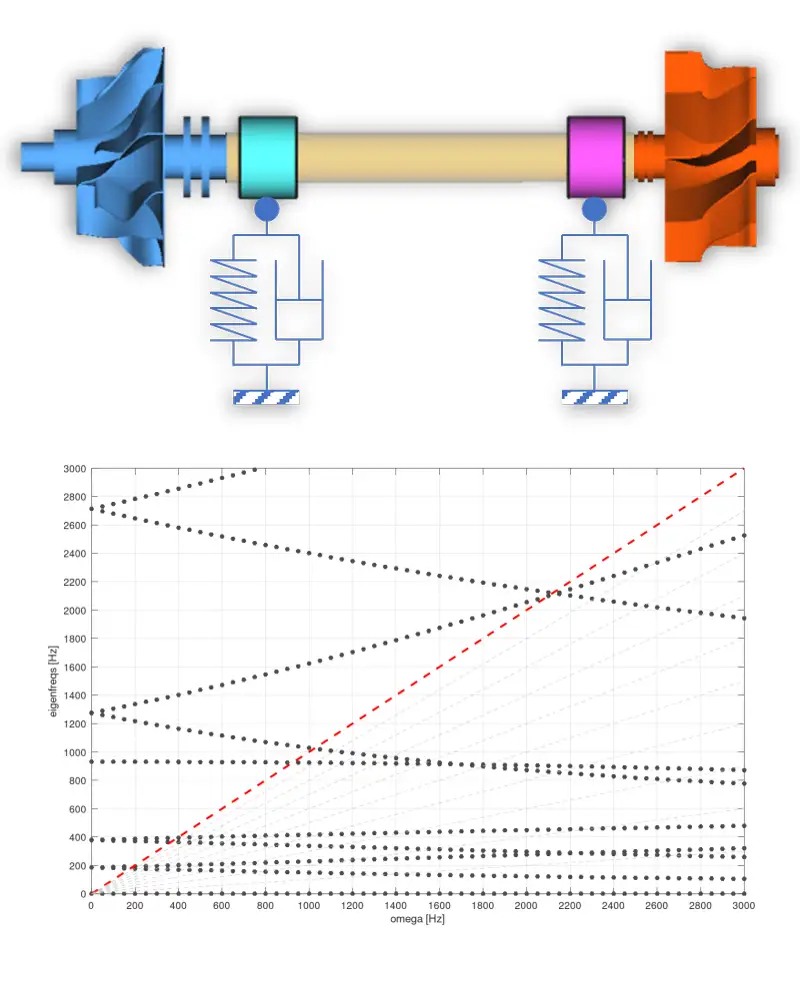
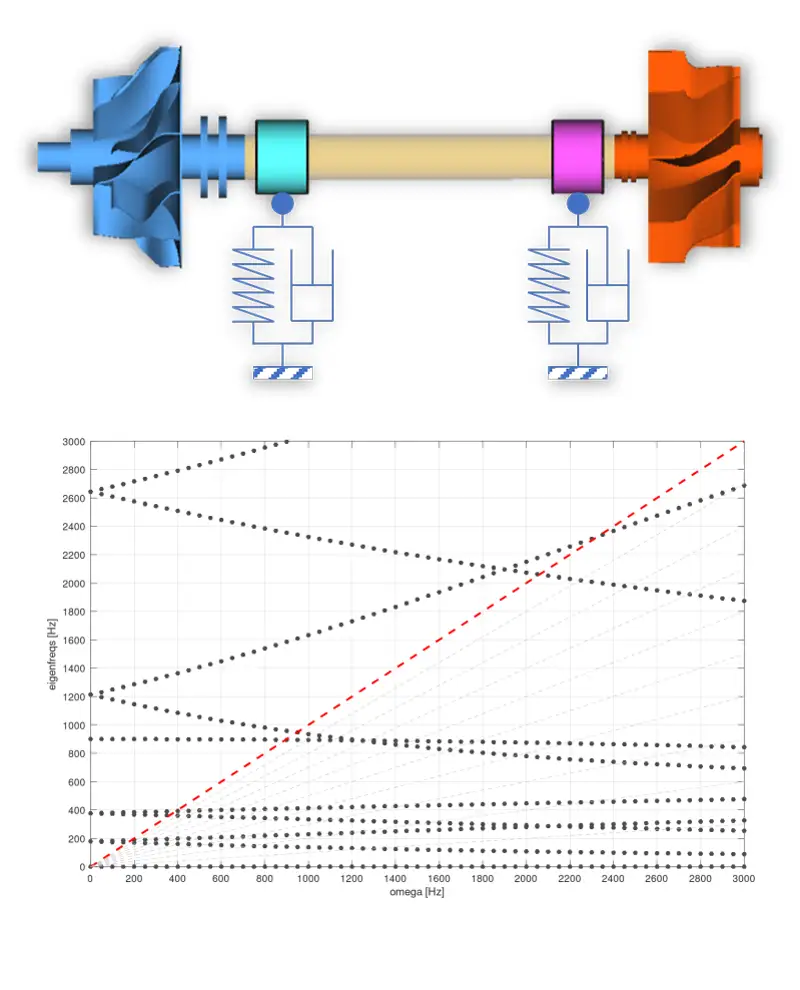
Folgendes Beispiel soll diesen Sachverhalt verdeutlichen. Dargestellt sind die Ergebnisse der Modalanalysen dreier Modelle in Form von Campbell-Diagrammen. Dabei werden die Eigenfrequenzen und die Erregerfrequenz des Systems über der Drehzahl aufgetragen und dient somit der Ermittlung von kritischen Betriebspunkten (Schnittpunkte der Eigenfrequenzen mit der Erregerfrequenz).
Ausgehend von einem Referenzmodell (Mitte) werden jeweils die Masse und Trägheit der Laufräder verringert (oben) bzw. die Lagersteifigkeit erhöht (unten). Beide Maßnahmen erhöhen die kritischen Drehzahlen. Die Variation der Lagersteifigkeit hat jedoch einen wesentlich größeren Einfluss auf die Systemdynamik als die Änderung der Masse bzw. Trägheit der Laufräder.
Aufgrund von Nichtlinearitäten in den Gleitlagern versagt die lineare Theorie im Hinblick auf die exakte Berechnung der Eigenfrequenzen. Sie erlaubt jedoch die Sensitivität einzelner Parameter zu untersuchen und gibt grobe Hinweise auf deren Auswirkung auf die Systemdynamik.
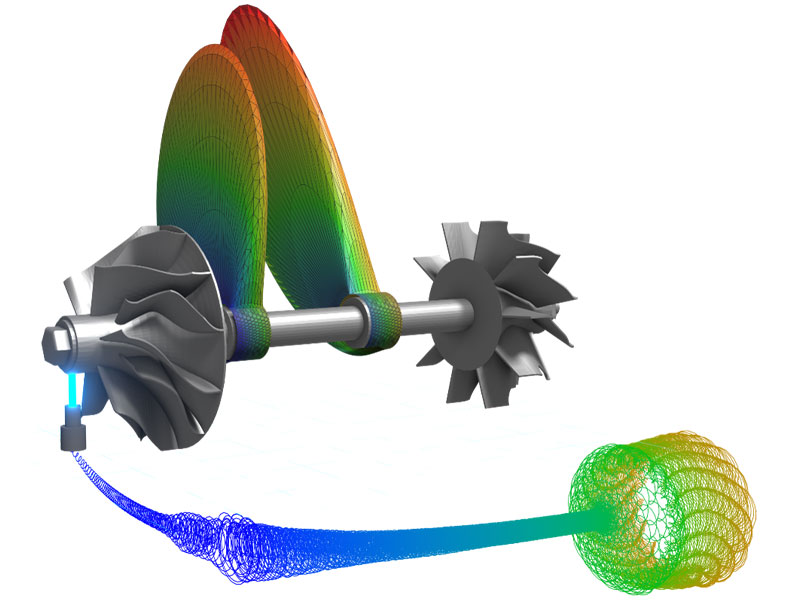
Modalanalyse mit gyroskopischem Einfluss
Transiente Hochlaufsimulation
Die Hochlaufsimulation ist ein recht einfaches Hilfsmittel, um das nichtlineare Verhalten von gleitgelagerten Rotoren abzuschätzen. Dabei wird das MKS-Modell des Rotors bis zu einer gewissen Grenzdrehzahl beschleunigt und das quasistationäre Schwingungsverhalten untersucht.
Der Betrieb von Turboladern erfolgt üblicherweise in einem Drehzahlbereich, in dem die drehzahlsynchronen und -asynchronen Schwingungen Instabilitätserscheinungen zeigen. Es entstehen schon ab einer geringen Drehzahl bereits selbsterregte Schwingungen unterschiedlicher Schwingungsformen bzw. Frequenzen.
Öldrucke innen/außen während einer Rotorumdrehung
Die Abbildungen zeigen die typischen Ergebnisse einer Hochlaufsimulation. Dargestellt sind die Exzentrizitäten der Schmierfilme (links) und das Campbell-Diagramm (rechts) der Vertikalschwingung gemessen am Verdichterrad. Man erkennt deutlich die sprunghafte Änderung der Lagerzustände. Diese Instabilitäten und Bifurkationen, die in hydrodynamisch gelagerten Rotoren auftreten, werden durch den Ölfilm induziert und führen zu den bekannten oil whirl und oil whip Phänomenen.
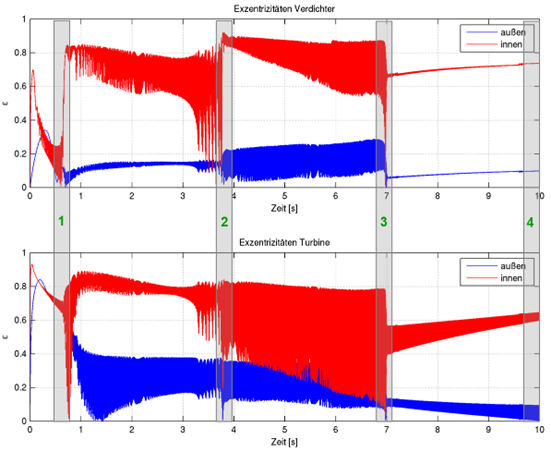

Lagerexzentrizitäten (links) FFT-Analyse der Rotorschwingung
Betrachtet man die Trajektorien der rotierenden Teile, lässt sich je nach Drehzahl und Zustand einen deutlichen Unterschied der Schwingformen erkennen.
Bei Rotoren mit Schwimmbuchsenlagerung können beide Ölfilme (innere und äußere) instabil werden. Diese Tatsache erklärt auch die subsynchronen Schwingungen, die typischerweise in solchen Systemen auftreten. Da die effektive hydrodynamische Winkelgeschwindigkeit im inneren Ölfilm größer ist als die im äußeren Ölfilm, treten die Bifurkationen auch bei unterschiedlichen Drehzahlen auf, wobei in der Regel der innere Ölfilm als erstes instabil wird.
Die Auswertung der Exzentrizitäten erlaubt weiterhin die Beurteilung und Abschätzung der Lagerzustände (kleinste Spalthöhe, spezifische Belastung des Radiallagers, Mischreibung, etc.). Anhand dieser Größen können aus der Simulation wichtige Erkenntnisse im Hinblick auf eine Grundauslegung der Lagerung gewonnen werden.
Schwingformen und Bahnkurven bei unterschiedlichen Drehzahlen
Fazit
Zusammenfassend lässt sich feststellen, dass die Modellierung und Simulation von gleitgelagerten Rotoren aus Sicht der Berechnung keine wesentlichen Probleme bereitet. Die notwendigen Modelle sind in Ihrer Komplexität überschaubar und sind mit Standartmethoden der Hydro- und Mehrkörperdynamik lösbar. Die wesentliche Schwierigkeit bereiten jedoch die Unkenntnis der notwendigen Randbedingungen bzw. gewisse Parameter des Systems. Beispielsweise sind die exakten Temperaturen innerhalb der Gleitlager weitgehend unbekannt und damit die Ölviskosität. Als weitere Schwierigkeit im Hinblick auf die Abstimmung der Modelle ist zum Beispiel die Unwucht des Rotors im Betrieb. Es ist eine entscheidende Größe, die sich in der Praxis kaum ermitteln lässt und sich von Rotor zu Rotor unterscheidet. Auch Näherungen in der Modellierungstiefe verursachen oft Abweichungen zwischen Messung und Simulation. Beispielsweise werden Kavitationserscheinungen mit analytischen Gleitlagerroutinen nicht berücksichtigt.
Im Hinblick auf die Auslegung und Optimierung von Turboladern sind zuverlässige Absolutaussagen mit Hilfe der Simulation nur in Einzelfällen möglich. Beschränkt man sich jedoch auf Relativaussagen, leisten die Simulationsmethoden einen wesentlichen Beitrag. Ausgehend von an Messungen abgestimmten Modellen, sind in Zusammenhang mit Produktentwicklung und -optimierung aufschlussreiche Parameterstudien und Sensitivitätsanalysen zuverlässig realisierbar.